在 DP 问题中我们将会着重的关注状态转移方程,同样地,在使用 BFS 对某些问题进行图论模型建模时,我们同样会关注状态转移。
BFS(Breadth-first Search),即广度优先遍历,在二叉树相关领域的题目中可能会经常碰到,Leetcode 中也有非常多关于二叉树层序遍历的问题,例如
- 199. Binary Tree Right Side View
- 102. Binary Tree Level Order Traversal
- 513. Find Bottom Left Tree Value
- 515. Find Largest Value in Each Tree Row
- ……
这些问题都可以借助队列这一数据结构使用层序遍历的方式解决。但是,这些问题并没有揭示 BFS 的一个非常重要的特性: 无权图最短路径求解方式。假定给你一棵二叉树,二叉树中部分节点中有专门“刀人”的邪恶机器人,再给定一个终止节点,问在该二叉树中是否存在一条从根节点到终止节点的最短路径。
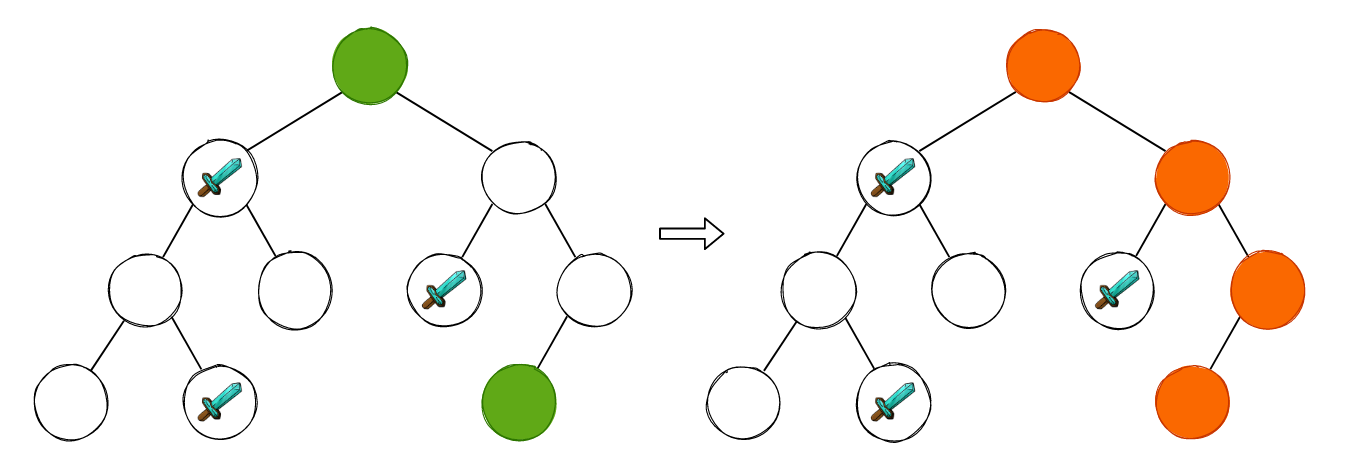
如上图所示,起点和终点使用绿色进行标识,我们也能够非常轻松的找到一条能到达终止节点的路径。在一棵二叉树中,只要能找到一条路径,那么它一定就是最短路径,因为再也没有其它路径能够到达该节点了。但是,一旦我们将这棵二叉树添加几条边,将其转换成一张图的话,事情就变得微妙了起来:
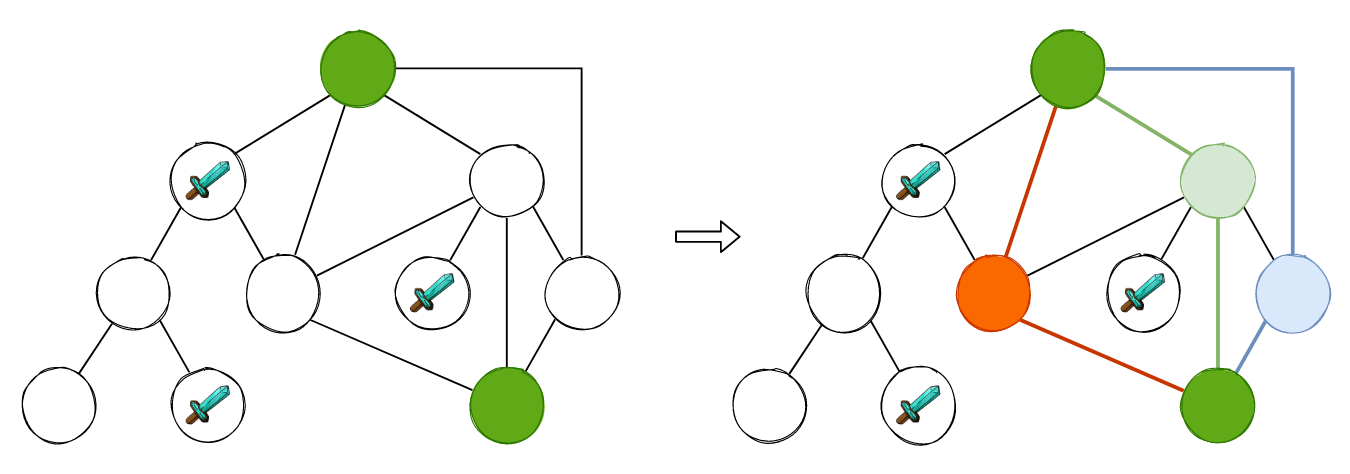
如上图所示,我们可以找到 3 条从根节点到终止节点的最短路径,也就是无权图的最短路径。那么为什么 BFS 就天然地能够解决无权图最短路径问题呢? 这是因为 BFS 的遍历过程中,是一层一层的进行遍历的,就像剥洋葱一样。当我们遍历到某一层找到了终止节点时,那么其余的最短路径一定在这一层,而不是下一层。这就好比我们下楼梯找东西,我们明明在第 4 层就找到了我们想要的,那么绝对不会再去第 3 层寻找。
1. BFS 的基本框架
相较于二叉树的层序遍历而言,图的 BFS 没有什么太大的区别,都需要借助队列这一数据结构实现,只不过因为图的 BFS 过程中可能会出现对节点重复访问的问题,所以我们需要添加一个 visited 数组,来帮助我们标记哪些已经遍历过的节点,从而避免重复访问:
void bfs(int src, int dst) {
vector<bool> visited;
queue<int> levelQueue;
visited[src] = true;
levelQueue.push(src);
while(!levelQueue.empty()) {
int size = levelQueue.size();
// 非常实用的小技巧,取出每一层的数据
for (int i = 0; i < size; i++) {
int current = levelQueue.front();
levelQueue.pop();
for (int neighbor: neighbors(current)) {
if (visited[neighbor]) continue;
visited[neighbor] = true;
// do something for child
levelQueue.push(child);
}
}
}
}
在上面的伪代码中,visited 数组使用 bool 型表示,我们同样也可以使用 int 来表示。例如 -1 则表示当前节点未曾访问过,大于 -1 则表示当前节点距离 src 节点的距离。如此一来我们不仅使用 visited 表示了节点是否被访问,同时也记录了每一个节点到 src 节点的距离,一举两得。
2. 直白的 BFS 问题
在文章开头所陈列的 Leetcode 上关于二叉树的 BFS 问题,个人更倾向于将其归类为“直白的 BFS 问题”,从题目描述中我们就能够很轻易的看出需要使用 BFS 进行求解。
例如 1091. Shortest Path in Binary Matrix,求仅包含 0 和 1 的二维矩阵中从左上角到右下角的最短路径距离,其中 1 表示障碍物,0 表示可行路径。这道题乍一看和 63. Unique Paths II 非常之类似,但是和 63 号问题不同的是,1091 号问题里面的“Robot”有 8 个前进方向,并且使用 DP 求解的时间复杂度必然是 O(n^2),而使用 BFS 求解则只需 O(V+E) 的时间复杂度,其中 V 为顶点个数,E 为边的个数。BFS 的过程如下图所示:

求解过程如下:
class Solution {
private:
int m, n;
vector<vector<int>> delta = {{-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}};
bool inGrid(int x, int y) {
return x >= 0 && x < m && y >= 0 && y < n;
}
public:
int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
m = grid.size(), n = grid[0].size();
if (grid[0][0] == 1 || grid[m-1][n-1] == 1) return -1;
if (m == 1 && n == 1) return 1;
queue<pair<int, int>> levelQueue;
vector<vector<int>> visited(m, vector<int>(n, -1));
levelQueue.push(make_pair(0, 0));
visited[0][0] = 1;
while (!levelQueue.empty()) {
pair<int, int> current = levelQueue.front();
levelQueue.pop();
int startx = current.first, starty = current.second;
for (int i = 0; i < 8; i++) {
int x = startx + delta[i][0], y = starty + delta[i][1];
if (inGrid(x, y) && grid[x][y] == 0 && visited[x][y] == -1) {
levelQueue.push(make_pair(x, y));
visited[x][y] = visited[startx][starty] + 1;
if (x == m - 1 && y == n - 1) return visited[x][y];
}
}
}
return -1;
}
};
3. 图论模型建模——状态转移
在 DP 领域中,有一个非常重要的概念: 状态转移方程,当我们面对一个 DP 问题的时候,只要找到了状态转移方程,基本上我们就认为已经解出了这个问题。在图论建模过程中,也存在状态转移这么个东西,只不过没有状态转移方程。
752. Open the Lock 要求我们求打开初始化状态为 "0000" 的密码锁,并且每次只能对 4 位密码锁中的一位往前拨或者是往后拨,同时存在一组 deadends,当我们的密码锁被拨到这些数字组合时,该密码锁将再也不能打开,求打开该密码锁所需最少的操作次数。
可以看到,这道题目就只是给了我们一个初始状态和一组“死亡数字”,既没有能够在 8 方向上移动的 Robot,也没有邻接矩阵、邻接表等能够代表图的东西。但是我们知道初始状态和结束状态,假设 target 为 "1234",那么我们就需要找到一条“路径”,从 "0000" 到 "1234",并且在该路径上不包含死亡数字。
对于 "0000" 来说,我们第一次的操作有 8 种选择: 选择哪一位,以及往前拨还是往后拨,如此一来,我们就可以得到:
- 往前拨:
"1000","0100","0010","0001" - 往后拨:
"9000","0900","0090","0009"
这样的一共 8 种状态,而得到的这 8 种状态每一种又可以得到 8 种状态,只不过 "0000" 需要从中剔除,所以是 7 种。如此一来我们就得到了一张图。为什么不是多叉树呢? 因为 "0000" 能到 "1000","1000" 也能到达 "0000"。
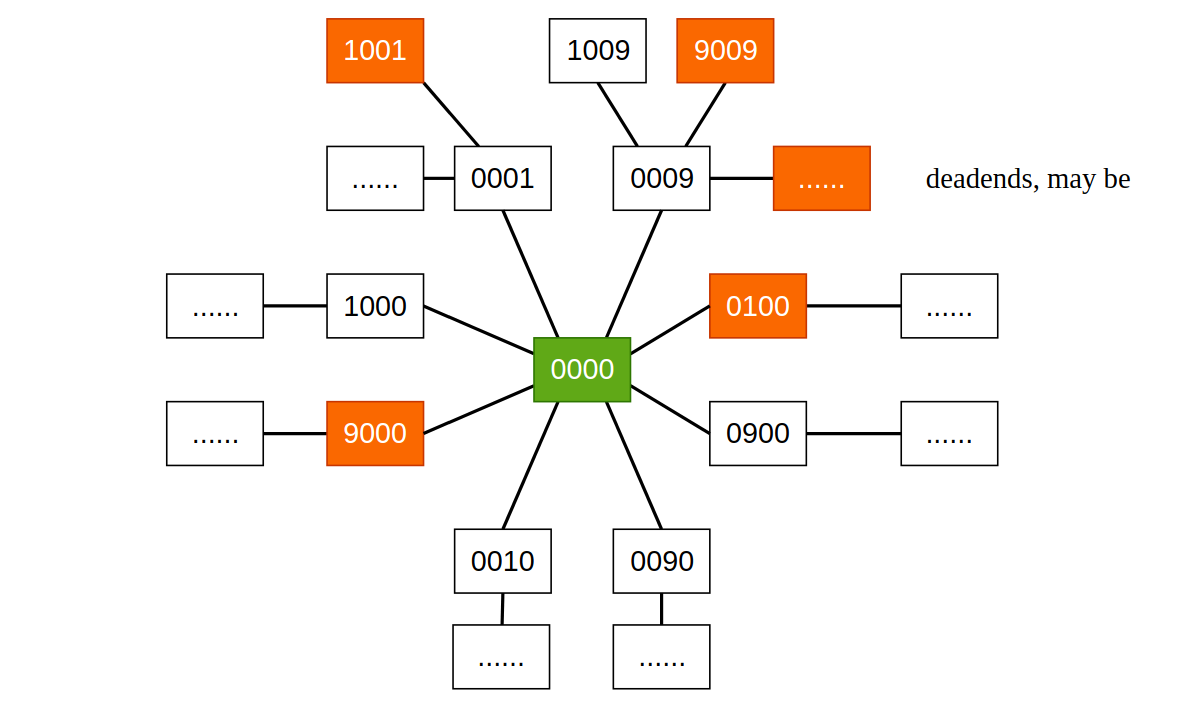
这其实就是自身状态的表达,每一个状态(例如"1000"、"0009")都是图中的一个顶点,从初始的状态一步一步地到达另外一个状态。本质上仍然可以看做是“Robot千辛万苦寻找家人”的问题。
题解可参考:
https://github.com/SmartKeyerror/Snorlax/blob/master/leetcode/bfs/752-Open-the-Lock.cpp
我们再来看另外一个智力问题:
有两个水桶,一个容量为 9 升,另一个容量为 4 升,如何操作能得到 6 升水?
依然使用状态转移对这个问题进行建模,我们有两个桶,所以初始状态可以表示为 "00",最终我们要得到 6 升水,那么结束状态可以表示为 "6x" 或者是 "x6",x 表示另一个桶有多少水我们并不关心,只要有一个桶里面有 6 升水就好了。
我们可以像上面那道打开密码锁一样,使用字符串的方式来表示状态,但是我们也可以使用 int 来表示。对于两个桶,使用 x 表示 9 升桶所容纳的水,y 则表示 4 升桶所容纳的水,那么状态即为 10x + y,一个用十位表示,另一个则用个位表示。如果有 3 个桶 x、y、z 的话,那么就可以使用 100x+10y+z 来进行表示。现在来看状态是如何转移的,假设当前两个桶的水量为 x、y。
最简单的两种操作就是将其中一个桶装满,或者是将其中一个桶中的水倒掉,那么状态可以表示为:
- 装满其中一个桶:
9 * 10 + y(装满 9 升桶),10x + 4(装满 4 升桶) - 倒掉其中一个桶:
0 * 10 + y(倒掉 9 升桶),10x + 0(倒掉 4 升桶)
另外一个操作就是将一个桶的水倒向另外一个桶内,情况稍微复杂一些:
- 将 9 升桶的水倒进 4 升桶:
10 * (9 - min(x, 4 - y)) + (y + min(x, 4 - y)) - 将 4 升桶的水倒进 9 升桶:
10 * (x + min(y, 9 - x)) + (y - min(y, 9 - x))
正如同状态转移方程之于 DP 问题一样,当我们找到全部的状态转移之后,就已经建立了 BFS 的图论模型,剩下的就只是按部就班的使用 BFS 求解即可。
int bucketPuzzle() {
queue<int> levelQueue;
// 使用 hashmap 判定是否访问过, value 为操作次数
unordered_map<int, int> visited;
levelQueue.push(0);
visited[0] = 0;
while (!levelQueue.empty()) {
int current = levelQueue.front();
levelQueue.pop();
int x = current / 10, y = current % 10;
vector<int> nextStatuses;
nextStatuses.push_back(9 * 10 + y);
nextStatuses.push_back(x * 10 + 4);
nextStatuses.push_back(0 * 10 + y);
nextStatuses.push_back(x * 10 + 0);
nextStatuses.push_back(10 * (9 - min(x, 4 - y)) + (y + min(x, 4 - y)));
nextStatuses.push_back(10 * (x + min(y, 9 - x)) + (y - min(y, 9 - x)));
for (int next: nextStatuses) {
if (!visited.count(next)) {
levelQueue.push(next);
visited[next] = visited[current] + 1;
if (next / 10 == 6 || next % 10 == 6)
return visited[next];
}
}
}
return -1;
}
如果需要输出详细的操作过程的话,添加一个 previous 数组即可,在数组中记录当前状态是从哪个状态而来的,而后遍历该数组逆序输出即可。
完整代码可参考:
https://github.com/SmartKeyerror/Snorlax/blob/master/leetcode/bfs/BucketPuzzle.cpp
4. 小结
BFS 由于天然地存在“无权图最短路径问题求解”这一特性,被广泛地应用在经典人工智能和搜索领域,包括我们所描述的水桶问题、打开密码锁问题,以及未提及的其它经典人工智能问题,本质上就是路径的搜索。
很多时候,可能我们并不能一眼看出某一个题目需要使用图论模型进行建模,而后使用 BFS 进行处理。但是一般来说,当题目中出现“最短”、“最少”、“最近”等关键词时,我们就可能需要考虑是否能够建立状态转移的模型,从而使用 BFS 进行求解。
