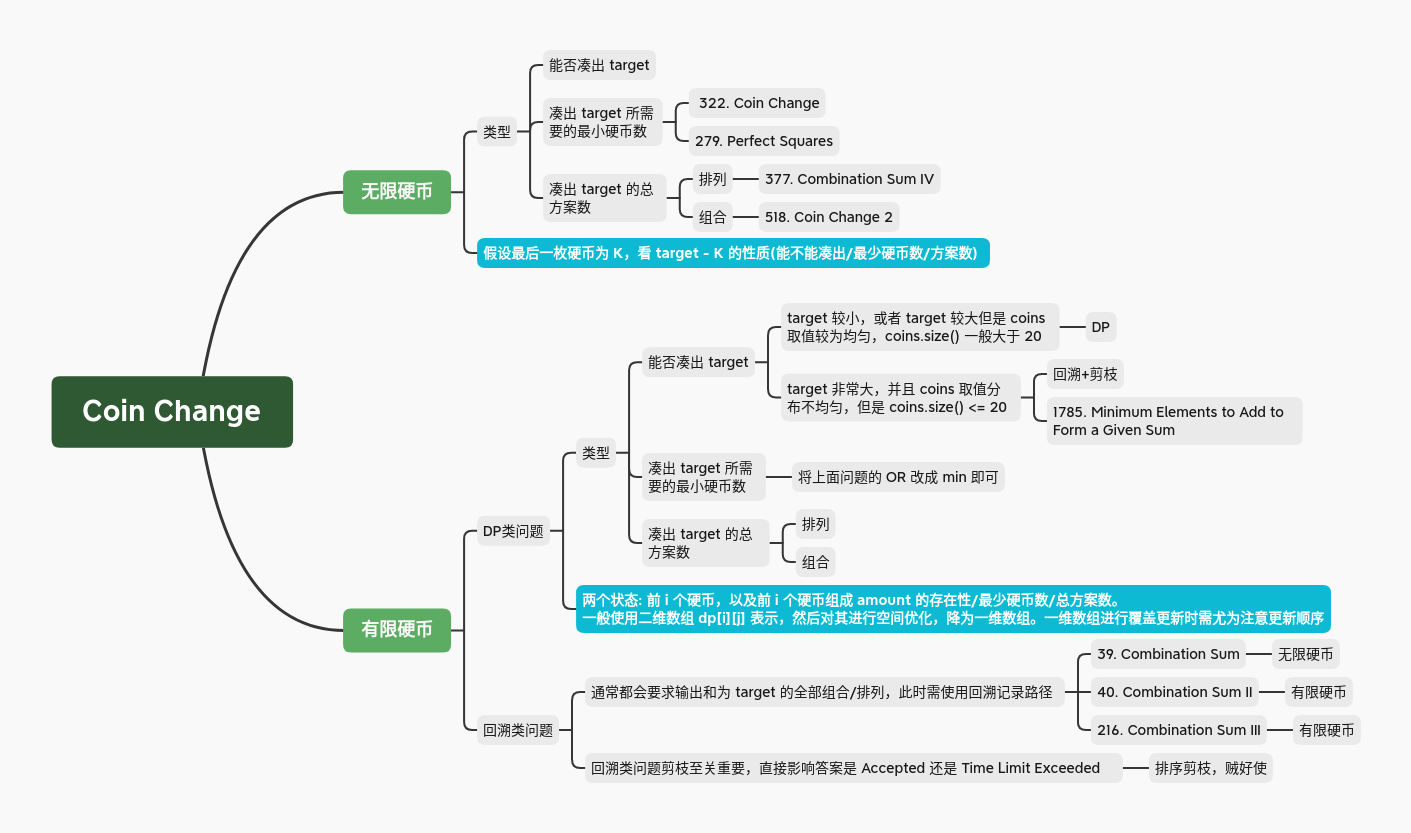
Coin Change 是一道动态规划问题中一道非常经典的题目,这是因为只要对原有的 Coin Change 问题稍加修改,就可以得到更复杂的动态规划问题,甚至是回溯问题。
1. 无限硬币
1.1 存在型动态规划
首先来看最简单的问题:
给定不同面额的硬币 coins 和一个总金额 amount,每一种硬币的数量是无限的,这些硬币能否组合成 amount? 若能组合,返回 true,否则返回 false。
类似于上面的问题,诸如求是否有某条路径/某个解决方案到达目标的问题,都可以被称之为存在型动态规划。再来看原问题,因为每一种面额的硬币数量是无限的,所以我们不知道能够组合成 amount 的方案中到底一共有多少个硬币。也就是说,这个问题与硬币数量无关,只和硬币的面额有关。
绝大部分的 DP 问题都是“自顶向下思考,自底向上实现”的。什么意思呢? 相较于第一枚硬币而言,我们更关注组成 amount 的最后一枚硬币,也就是拼成完整拼图的最后一块儿。假设硬币面额为 [2, 3, 5],amount 为 11,并且组成 amount 的最后一枚硬币面额为 K。那么如果我们知道了 amount-K 能不能被 coins 拼出来,也就知道了整个问题的答案。
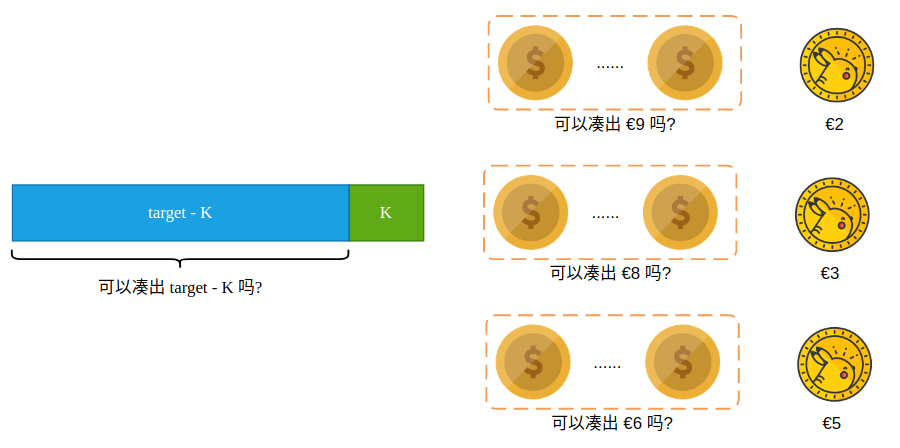
在最后一枚硬币面额为 K 的情况下,如果我们能拼出 amount-K 的话,那么再加上最后一枚硬币 K,总金额刚好为 amount,结果为 true。反之,如果我们不能拼出 amount-K 的话,结果为 false。可以看到,本来题目是要求能不能拼出 amount,但是现在需要知道能不能拼出 amount-K,这就是一个规模更小的问题,也就是子问题。代码实现如下:
bool solution(vector<int>& coins, int amount) {
vector<bool> dp(amount + 1, false);
// 当总金额为 0 时我们一个硬币都不选,所以为 true
dp[0] = true;
// 计算金额为 1、2、3...amount 能否由 coins 拼出,sub 即为子金额
for (int sub = 1; sub <= amount; sub++) {
// 每一枚硬币都作为最后一枚硬币,看能不能拼出 sub - coin
for (int coin : coins) {
// 简单的来看,sub - coin 必须大于等于 0,才能作为数组下标
if (sub >= coin) {
dp[sub] = dp[sub] || dp[sub - coin];
}
}
}
return dp[amount];
}
1.2 最值型动态规划
接下来看最值型的动态规划问题,仍然是硬币找零,这次使用 LeetCode 上的原题: 322. Coin Change,问题描述如下:
给定不同面额的硬币 coins 和一个总金额 amount,你可以认为每种硬币的数量是无限的。写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
这个问题在第一个问题之上难度增加了一点点,问凑成 amount 需要的最少硬币数,硬币仍然是无限供应。同样的,由于硬币是无限供应的,所以我们不能考虑硬币数量,而是要考虑最后一个硬币的情况。
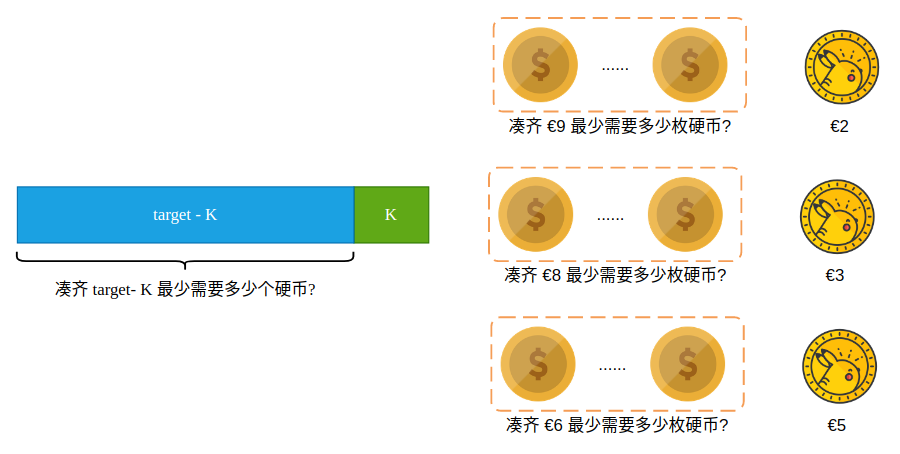
仍然假设最后一枚硬币面额为 K,那么现在如果我们知道了凑成 amount-K 所需要的最少硬币数的话,也就知道了当最后一枚硬币为 K 时凑出 amount 所需要的最少硬币数。这同样是一个规模更小的问题,也就是子问题。
int solution(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX);
// 当金额为 0 时一枚硬币都不需要,所以 dp[0] = 0
dp[0] = 0;
for (int sub = 1; sub <= amount; sub++) {
for (int coin : coins) {
if (sub >= coin && dp[sub - coin] != INT_MAX) {
dp[sub] = min(dp[sub], dp[sub - coin] + 1);
}
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
1.3 组合数型动态规划
组合数型的动态规划通常需要求达成某一个目标的所有方案数,比如说凑够 amount 一共有多少种凑法。这类问题的关键点不在于状态转移方程如何思考,而是在于明确到底是组合数还是排列数。
例如 1 + 2 + 1 和 1 + 1 + 2 到底是算一种组合方式,还是两种。有的题目会明确告知是计算排列数还是组合数,有的题目则会在 Example 中通过具体的案例告诉我们到底是组合还是排列。
首先来看排列问题,因为 1 + 2 + 1 和 1 + 1 + 2 是两种不同的方式,所以这和最后一个硬币到底是谁有关系。假如最后一个硬币面值为 1、且 amount = 4 的排列方式有 3 种,最后一个硬币面值为 2、且 amount = 4 的排列方式有 2 种,加起来一共 5 种。此时我们就可以说当 coins = [1, 2] 且 amount 为 4 时总的方案数为 5。

所以说,排列问题仍然是让每一枚硬币都作为 Last Coin,然后看 amount-K 有多少种凑法,实现如下:
int solution(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, 0);
// 哪个硬币都不要,也是一种排列方式
dp[0] = 1;
for (int sub = 1; sub <= amount; sub++) {
// 每一种不同面额的硬币作为 Last Coin 计算方案数
for (int coin : coins) {
if (sub >= coin)
dp[sub] += dp[sub - coin];
}
}
return dp[amount];
}
LeetCode 中的 377. Combination Sum IV 其实就是一道求排列总方案的 Coin Change 问题。题干中并没有直接的使用 “permutation” 一词,而是在 Example 中说明了该题其实是一道排列型问题。
再来看组合问题,也就是 1 + 1 + 2 和 2 + 1 + 1 属于同一种凑法,所以只和金额有关系,谁是最后一个硬币 Who Care。那么此时我们就需要金额作为最后一块儿拼图,硬币面值作为已有的拼图。也就是说,我们计算的是当我们只有面额为 [1] 的硬币时凑成 amount 的方案数,只有面额为 [1, 2] 时凑成 amount 的方案数,只有面额为 [1, 2, ...] 的硬币凑成 amount 的方案数。实现如下:
int solution(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, 0);
// 同样的,哪个硬币都不选,也是一种组合方式
dp[0] = 1;
for (int coin : coins){
for (int sub = 1; sub <= amount; sub++){
if (sub >= coin)
dp[sub] += dp[sub - coin];
}
}
return dp[amount];
}
2. 有限硬币
对于无限硬币的 DP 问题来说,当我们假设最后一枚硬币为 K 时,凑齐 amount-K 时依然可以使用最后一枚硬币的面值,所以在计算子问题时对于硬币是怎么排列的,使用过了哪些硬币完全可以忽略。但是,当每一种面额的硬币均只有一枚时,情况将截然不同。当我们以 K 作为最后一枚硬币时,前面的 target-K 将不能再使用该枚硬币,也就是说,我们需要关心使用了哪些硬币。
2.1 存在型动态规划
给定不同面额的硬币 coins 和一个总金额 amount,每一种硬币只能使用一次,这些硬币能否组合成 amount? 若能组合,返回 true,否则返回 false。
前面提到过,当我们失去“无限硬币”这个外挂以后,我们便不能将子问题定义成“能否拼出amount-K”了,因为在计算 amount-K 时完全有可能将最后一枚面额为 K 的硬币也算进去,但实际上面额为 K 的硬币可能只有一枚。
对于 coins 中的每一枚硬币,状态其实只有两种: 选择该枚硬币和不选该枚硬币。也就是对于最后一枚 K 来说,我可以选择这一枚硬币,然后看前 n-1 枚硬币能不能拼出 amount-K出来。或者说我们不选择该枚硬币,那么就得看前 n-1 枚硬币能不能拼出 amount 了。
本来我们是要求 coins 这 n 枚硬币能否拼出 amount,现在我们从 coins 的最后一枚硬币出发,得到了一个“二分选择”,也就是看前 n-1 枚硬币能不能拼出 amount-K 或者是拼出 amount。如果这两种情况都是 false 的话,那么整个问题就是无解的,也就是应该返回 false。这样我们就得到了一个规模更小的问题(n 枚硬币变成了 n-1 枚硬币),也就是子问题。
这其实就是 0-1 背包的核心思想: 选还是不选,这是一个问题。
好了,我们使用“前 n-1 枚硬币能否…”这样的方式来杜绝我们对同一枚硬币的重复选取,所以说硬币的数量也将作为我们的状态,当然,还有 amount。所以,我们使用 dp[i][sub] 来表示前 i 枚硬币能否凑出金额 sub。实现如下:
bool solution(vector<int>& coins, int amount) {
int n = coins.size();
vector<vector<bool>> dp(n + 1, vector<bool>(amount + 1, false));
// 前 0 枚硬币当然可以组成金额 0,因为一枚硬币都没有
dp[0][0] = true;
for (int i = 1; i <= n; i++) {
for (int sub = 1; sub <= amount; sub++) {
// 前 i 枚硬币的最后一枚硬币为 i-1,面额为 coins[i-1]
int lastCoin = coins[i-1];
if (sub >= lastCoin)
dp[i][sub] = dp[i-1][sub] || dp[i-1][sub-lastCoin];
else
// 当最后一枚硬币的面值比金额还要大时候,我们肯定不能选择该枚硬币
dp[i][sub] = dp[i-1][sub];
}
}
return dp[n][amount];
}
在继续往下之前我们先来看一个 DP 问题非常重要的组成: 空间优化。当我们需要使用二维数组才能解决问题时,第一个反应就是能不能使用一维数组进行优化。如下面这条核心语句:
dp[i][sub] = dp[i-1][sub] || dp[i-1][sub-lastCoin];
如果将 dp[i][sub] 想象成一个二维矩阵的话,第 i 行只与第 i-1 行有关系,那么我们完全可以只使用 2 行来进行滚动更新。比如说我们可以用第一行来计算当 i 为奇数时的情况,第二行来计算当 i 为偶数的情况,如下图所示:
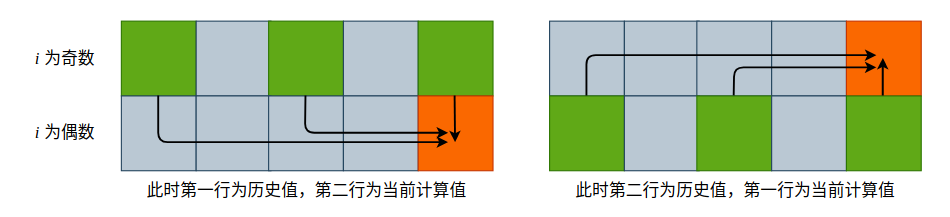
我们只需要将原来的 dp[i] 换成 dp[i%2] ,将 dp[i-1] 换成 dp[(i-1)%2] 即可,其它的逻辑照抄,就能实现只使用两行空间完成计算。
bool solution(vector<int>& coins, int amount) {
int n = coins.size();
vector<vector<bool>> dp(2, vector<bool>(amount + 1, false));
dp[0][0] = true;
for (int i = 1; i <= n; i++) {
for (int sub = 1; sub <= amount; sub++) {
int lastCoin = coins[i-1];
if (sub >= lastCoin)
dp[i%2][sub] = dp[(i-1)%2][sub] || dp[(i-1)%2][sub-lastCoin];
else
dp[i%2][sub] = dp[(i-1)%2][sub];
}
}
return dp[n%2][amount];
}
更丧心病狂一些,我们也可以只使用一行空间来进行覆盖更新,将这个一维数组分成新值和旧值,当利用完旧值计算好了新值以后,用新值直接覆盖掉旧值,俗称过河拆桥。
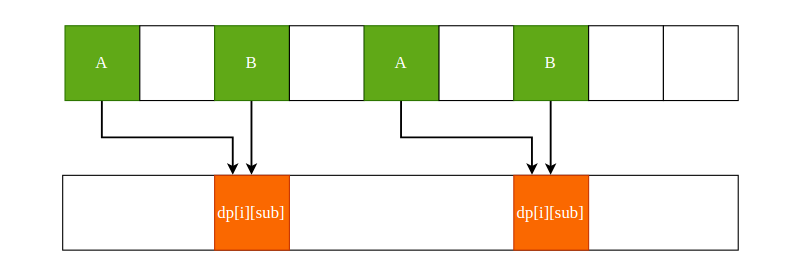
如上图所示,在二维空间中 dp[i][sub] 的值依赖于其正上方的值以及其左上方的值。所以说,当我们使用一维数组进行覆盖更新时,sub 需要从右向左遍历,这样一来 dp[i-1][j] 和 dp[i-1][j-lastCoin] 的值才不会被新值所覆盖。
bool solution(vector<int>& coins, int amount) {
int n = coins.size();
vector<bool> dp(amount + 1, false);
dp[0] = true;
for (int i = 1; i <= n; i++) {
// 覆盖更新必须从右向左,因为左边儿的值还得用到呢
for (int sub = amount; sub >= 1; sub--) {
int lastCoin = coins[i-1];
if (sub >= lastCoin)
dp[sub] = dp[sub] || dp[sub-lastCoin];
}
}
return dp[amount];
}
Leetcode 中 416. Partition Equal Subset Sum 就是一道有限硬币的存在型问题。只不过题目描述的比较隐晦,问一个数组能不能被分成两个元素和相等的子集,其实就是在问一个数组能不能找到一个子集,使其和为 sum(nums) / 2。
值得一提的是,动态规划并不适用于所有的存在性硬币问题,这和我们需要解决问题的数据规模,准确的来说,和 amount 以及 coins 的分布相关。当 amount 较小时,例如 5000、100000,由于 C++ 底层对于 vector<bool> 进行特殊的内存分配管理,使得我们开大小为 10 万的 vector<bool> 代价不是很高。
但是,一旦 amount 的值变得巨大,例如 10^9,并且 coins 的取值范围跨度非常之大,例如 [1, 2, 45256, 2014896],这个时候不应该使用动态规划的思想来求解存在型问题,而应该使用回溯+剪枝的方式实现。1780. Check if Number is a Sum of Powers of Three,这道题目就是一个典型,amount 的取值达到了 10^7(原题目为 n,可以看作是 amount)。但是 coins 的数量却很少,因为 3^20 其实就已经远超出了 amount 的范围。
关于这道问题的题解可参考:
2.2 最值型动态规划
给定不同面额的硬币 coins 和一个总金额 amount,每一种硬币只能使用一次,组合成 amount 最少需要几枚硬币? 如果没有任何一种硬币组合能组成总金额,返回 -1。
分析过程和存在型动态规划一样,由于每一种面额的硬币只能使用一次,所以硬币的数量需要考虑在内。设 dp[i][sub] 表示前 i 枚硬币凑成金额 sub 所需要的最少硬币数,要么是前 i-1 枚硬币凑成 sub,要么是前 i-1 枚硬币凑出了 sub-coins[i-1] ,再加上最后一枚硬币凑成了 sub。
dp[i][sub] = min(dp[i-1][sub], dp[i-1][sub-coins[i]] + 1);
优化过程类似,首先我们使用二维数组求解,然后用滚动数组将空间优化至两行,进而使用一维数组进行覆盖更新,优化后代码如下:
int solution(vector<int>& coins, int amount) {
int n = coins.size();
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int i = 1; i <= n; i++) {
for (int sub = amount; sub >= 1; sub--) {
int lastCoin = coins[i-1];
if (sub >= lastCoin && dp[sub-lastCoin] != INT_MAX)
dp[sub] = min(dp[sub], dp[sub-lastCoin] + 1);
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
可以看到,只需要对存在型问题的解稍加修改即可得到最值型问题的答案。在使用一维数组进行覆盖更新时,一定要准确的理解为什么第二层循环要从右向左遍历。
2.3 组合数型动态规划
和存在型与最值型问题基本类似,对状态的定义稍加修改即可,故不再赘述。
3. 小结
Coin Change 类问题既可以看作是 0-1 背包问题,也可以看作是完全背包问题,不过他们的本质都是一样的: 对于第 K 个硬币/物品来说,在无限硬币中我们可以选择一个都不放和放多个,在单一使用硬币中我们可以选择放和不放,动态规划中一大类问题都可以使用 Coin Change 以及 0-1 背包问题解决。
动态规划和回溯是一对好兄弟,有时候不适合使用动态规划解决的问题,使用回溯法或许能有意外之喜。不过,这通常与输入数据的规模与分布有关。
Leetcode 上 Coin Change 类问题:
(1) 无限硬币
(2) 有限硬币