在《算法》(第四版)的第一章最后一小节中, 也就是”案例研究: union-find算法”这一小节, 我看到了并查集。 在我完整的阅读了所有的算法内容之后, 脑子里只剩下两个字: 优美。
1. 为什么需要union-find算法
小A的人际关系非常之广, 拥有非常多的朋友, 同时, 他的朋友也有很多朋友。 如果两个人是朋友关系的话就记为a-b。
小A的人际关系可以表示为: A-C A-E A-F A-P A-M A-O A-K…而他的一些朋友的人际关系可以表示为 S-W M-I M-O M-T O-Y O-C E-G…小A朋友的朋友的人际关系可以表示为 K-P K-B X-U Z-O…
通过这样的方式整理出了小A的所有人际关系连接, 以及小A的朋友的人际关系连接。 现在我想要知道, 某一位同学能不能推荐给小A。 例如A-C C-F, 小C是A, F的共同好友, 尽管A, F两人不是朋友关系, 但是由于小C这层枢纽的存在, 很有可能使得他们成为朋友。 也就是说, 需要判断A, F两者之间的连通性, 从而生成推荐朋友的功能。
在一个大型网络系统中, 如果节点A与节点C连接, 记为A-C。 如果节点A既与节点C由于节点B连接的话, 我们可以说节点B和节点C是连接的。 给定相当数量节点连接情况, 判断出系统中任意两个节点是否连接。
很明显的, union-find算法就是解决这一类问题的: 动态连接问题。 连接问题在上面已经描述过了, 那么动态是什么意思? 人和人之间的人际关系不是一成不变的, 系统中节点的连接状态也不是一成不变的。 在某些情况下, 两个完全不相关的人成为了朋友, 此时我们就需要处理这些连接, 并重新判断连接性, 这就是动态性。
2. 设计union-find算法
既然是解决系统中的连接性, 那么最基本的API就是判断两个元素是否处于连接状态, 如果两个元素的标识位是相同的, 我们就可以判断它们是连通的, 所以需要额外的一个查找API。 此外, 还要提供将两个元素连接的API。
那么整体的API设计就是这样:
public class UnionFind:
UnionFind(int N) // 初始化节点
void union(int p, int q) // 连接p, q
int find(int p) // 查找p的标志位
boolean connected(int p, int q) // 判断p, q是否连接
整体的算法基于什么样的基本数据结构呢? 数组, 链表还是树? 数组的下标以及数组中所存储的元素会有一种对应。 例如data[0] = 1, 我们可以认为0这个节点的标识是1。 如果又有data[12] = 1, 节点12的标识位也是1, 此时可以判断节点0和节点12是连接的。
如果采用数组实现, 连接p, q两个节点又该如何操作? 一个非常简单的做法就是将节点p的标志位设置为节点q的标志位, 使两者的标识位同步即可。
在数组初始化的时候就有:

那么UnionFind类的初始化过程就非常简单了, 申请容量为N的数组, 逐一赋值即可:
public class UnionFind:
private int[] data;
UnionFind(int N) {
data = new int[N];
for(int i = 0; i < N; i++) {
data[i] = i;
}
}
2.1 quick-find算法
quick-find算法的思路是这样的: 使用数组的索引作为节点, 数组索引所对应的值作为节点标识。 在连接p, q两个节点时, 首先查找p, q两个节点的标识位, 将所有与p连接的节点的标识位改为q的标识位。 图示过程如下:
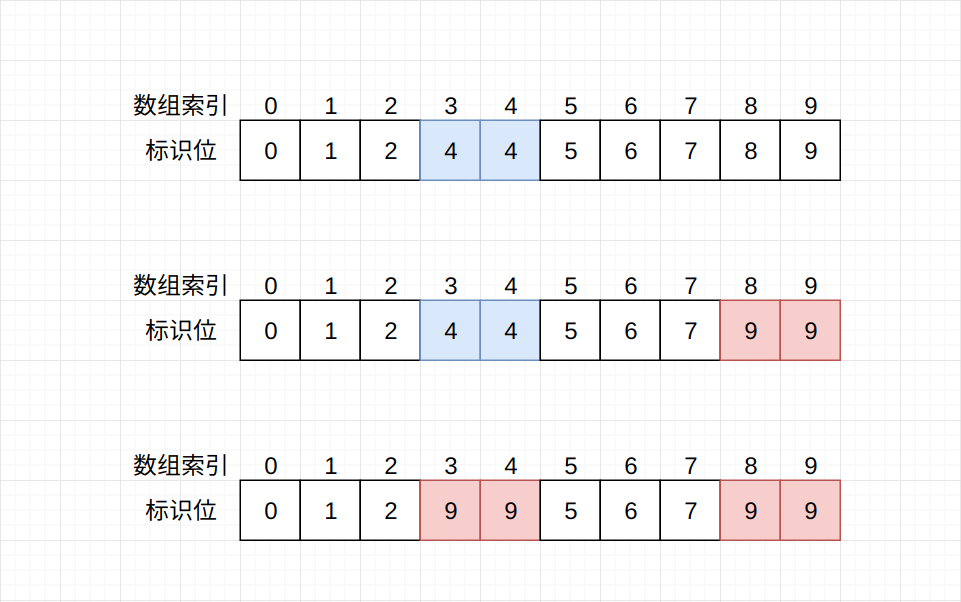
public int find(int p) {
return data[p]; // 返回节点p的标志位
}
public void union(int p, int q) {
int pID = find(p);
int qID = find(q);
if (pID == qID) return;
// 遍历所有与节点q标识位相同的节点, 并将其标识位改为q的标识位
for (int i = 0; i < data.length; i++) {
if (data[i] == pID)
data[i] = qID;
}
}
为什么这个算法称为quick-find呢? 因为在查找过程中, 采用的是直接取数组下标的方式, 时间复杂度为O(1), 而union操作则需要遍历整个数组, 其时间复杂度为O(n)。
2.2 quick-union算法实现
虽然quick-find算法拥有较高的查找效率, 但是其union操作效率较低, 所以通常会使用quick-union算法来实现并查集。
quick-union算法的思路是将每一个元素看成是一个节点, 将数组整理成为一个树结构, 并由孩子节点指向父亲节点。
在初始化数组的时候, 我们说数组的索引代表了节点本身, 而数组的索引值代表了节点的标识位。 而现在, 数组的索引值不再代表节点的标识位了, 而是代表其父节点。
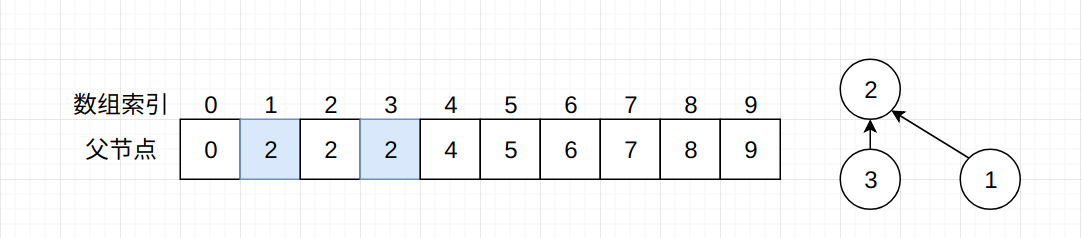
如上图所示, 首先我们将节点3与节点2连接, 按照孩子指向父亲的原则, data[3] = 2。 再将节点1与节点3进行连接, 此时节点3不直接与节点1进行连接, 而是与节点1的父亲节点进行连接, 也就是节点2, 所以就有data[1] = 2。
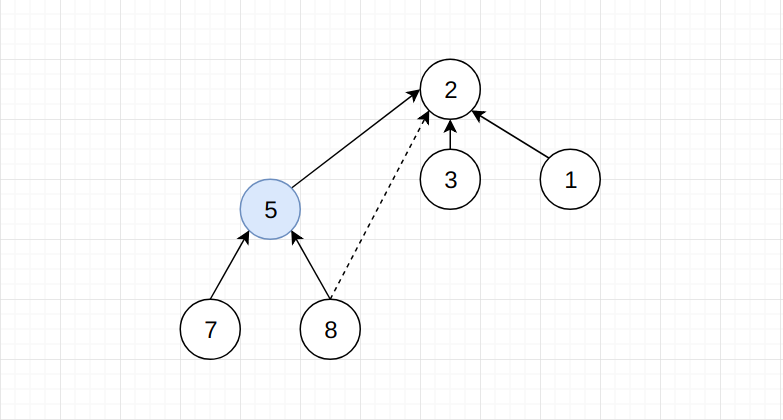
在上图中, 我们让节点8和节点2进行连接, 它们不会直接连接, 因为节点8还有父节点5, 让节点5和节点2进行连接。 由于节点5和节点2都是父节点, 所以节点5可以直接指向节点2。 此时数组内的数据情况为:
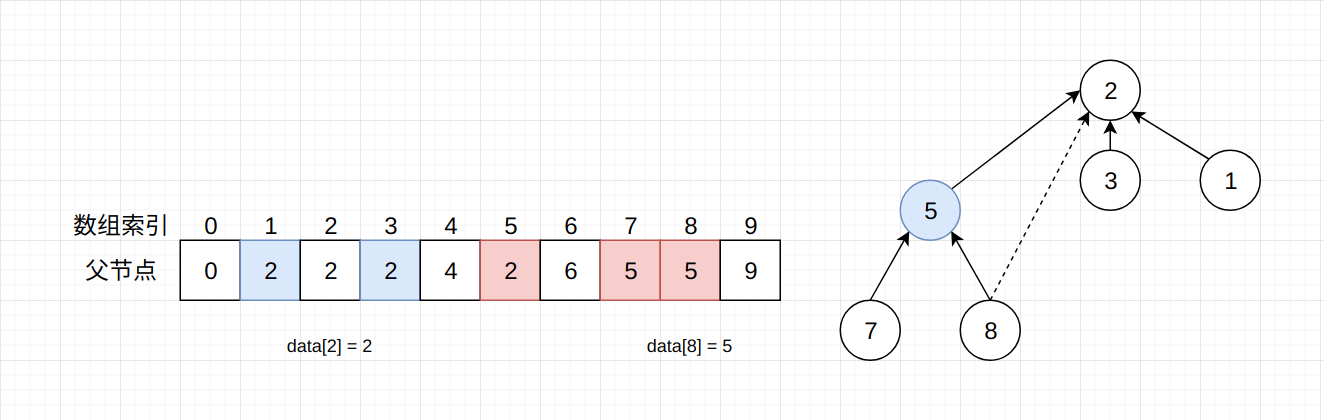
public int find(int p) {
// 循环查找父节点
while (p != data[p])
p = data[p];
return p;
}
public void union(int p, int q) {
// 此时find操作得到的结果是两个节点的根节点
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) return;
data[pRoot] = qRoot; // 使p的父节点指向q的父节点
}
3. quick-union算法的优化
3.1 基于树高的优化
B-Tree之所以非常高效的原因, 是因为其树高最多只有4层(树叶因子如果是500的话, 此时可容纳250T的数据), 那么对于我们的数组树结构来说, 虽然没有指针, 但是逻辑上仍然是一颗树, 所以对树高的优化非常有必要。
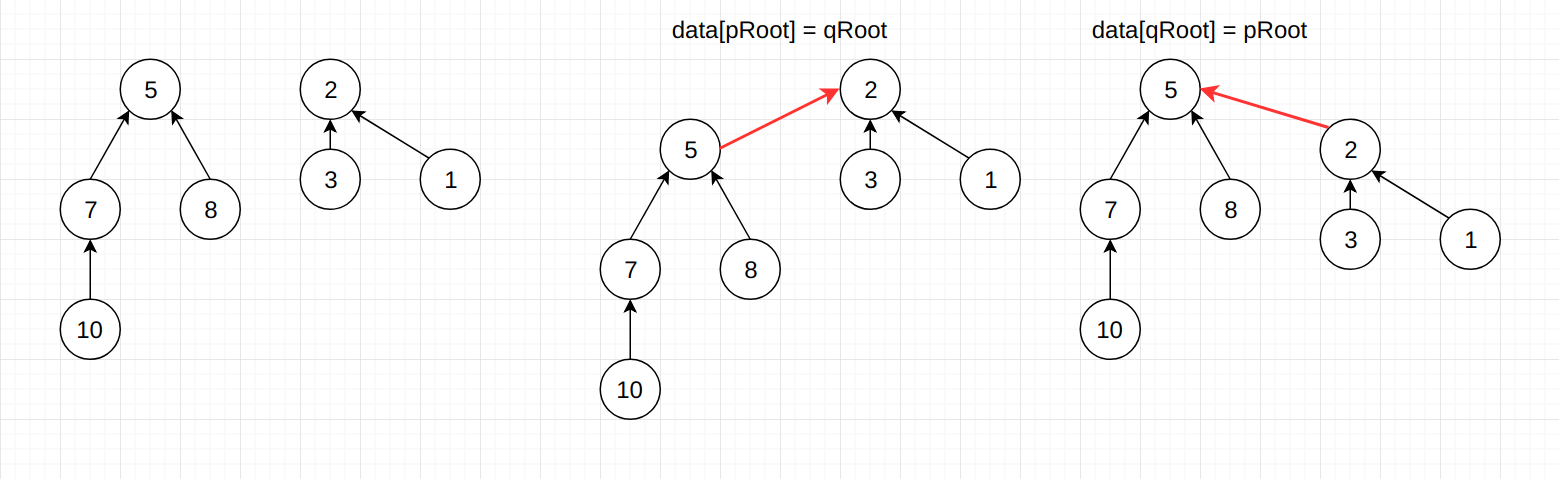
如上图所示, 如果是左侧根节点指向右侧根节点的话, 整体树高为4。 而如果是右侧根节点指向左侧根节点的话, 整体树高为3。 所以我们需要额外的增加一些数据, 来记录每棵树的树高。
public class UnionFind:
private int[] data;
private int[] rank;
UnionFind(int N) {
data = new int[N];
rank = new int[N]
for(int i = 0; i < N; i++) {
data[i] = i;
rank[i] = 1; // 初始化时每棵树的高度均为1
}
}
那么在union方法中, 就需要进行一些比较。 将树高低的指向树高高的即可。
public void union(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) return;
if (rank[pRoot] < rank[qRoot])
data[pRoot] = qRoot;
else if (rank[pRoot] > rank[qRoot])
data[qRoot] = pRoot;
else { // 当两棵树的树高相同时, 谁指向谁都一样, 树高必定会增加
data[pRoot] = qRoot;
rank[qRoot] ++;
}
}
3.2 路径压缩
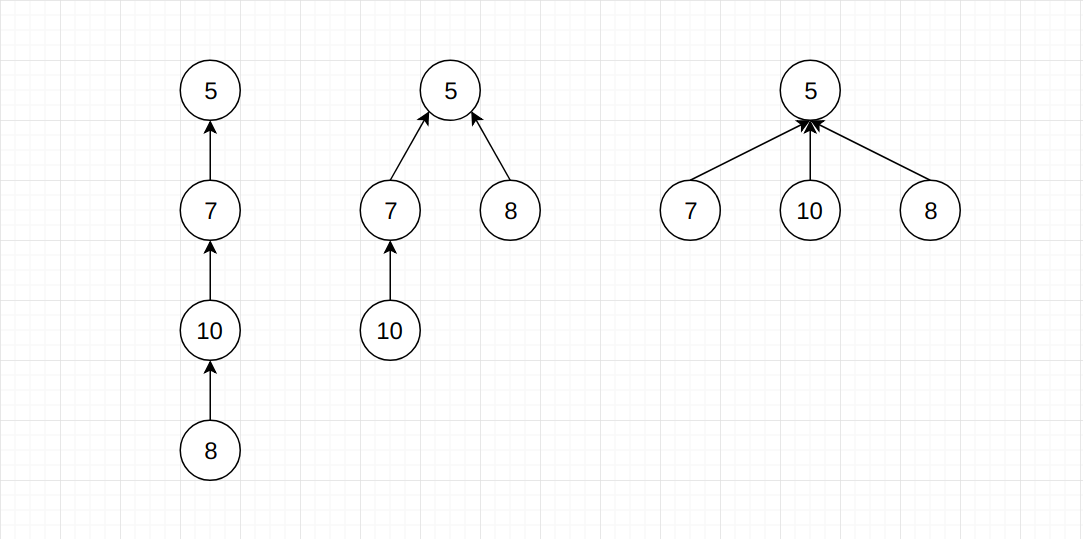
图中3种树结构都表达了同一个意思, 节点5, 7, 10, 8互相连接, 且根节点都为5。 虽然表达的意思相同, 但是它们在union和find操作上的效率却不尽相同。 很明显的, 最右侧的树有着最高的操作效率, 这也是路径压缩需要做的事情。
这个过程其实很简单, 只需要执行data[p] = data[data[p]]即可。 也就是说, 让某一个节点指向父节点的父节点, 这样一来树高就能减少一层。
public int find(int p) {
while (p != data[p]) {
data[p] = data[data[p]];
p = data[p];
}
return p;
}
4. 小结
union-find算法主要是为了解决连通问题, 从实际角度上来讲, 使用频率并不是很高。 但是其利用数组所构建的树结构却是整个算法最为精妙的部分, 同时也体现出了数组这个基本数据结构的强大威力。